Шахматный турнир
Четыре шахматиста Антонюк, Григоров, Даринцев и Маричев решили устроить между собой шахматный турнир. По условиям соревнования предполагалось, что каждому из них предстоит состязаться по очереди с другими тремя. Состязание каждой пары шахматистов продолжается до первой победы одного из соперников (ничьи не считаются).
Очки участники турнира решили подсчитывать таким способом: каждый получает по одному очку за каждую победу побежденного им соперника.
Распределение мест в турнире было решено производить традиционным способом: победителем будет считаться участник состязания, у которого окажется наибольшее число очков (если таковых окажется несколько, то все они будут признаны чемпионами).
После завершения турнира оказалось, что Григоров проиграл встречу Маричеву но все же оказался единственным победителем соревнования. Даринцев же занял последнее место.
Каков был результат трех встреч, проведенных Антонюком?
Антонюк победил Даринцева и Маричева и проиграл Григорову.
Поскольку в турнире каждый шахматист встречается с остальными тремя и результат каждой такой встречи — победа одного из соперников, то победителем турнира может быть шахматист, победивший по крайней мере в одной встрече и набравший при принятых условиях подсчетане меньше, чем одно очко. Докажем это.
Пусть на рисунках 1 и 2 изображены два возможных исхода встреч трех шахматистов. На этих рисунках кружочками изображены участники шахматного турнира, а направления стрелок указывают победителя соответствующей парной встречи.
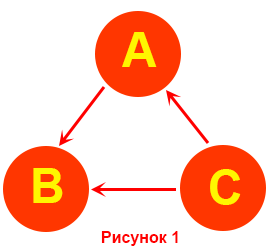
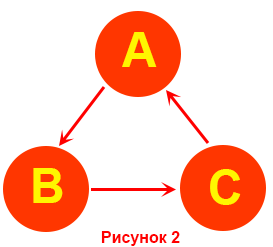
В случае, изображенном на рис. 1, на звание победителя может претендовать шахматист В, набравший 1 очко. В случае же, представленном на рис. 2, ни одному из шахматистов очки не начисляются Однако после игры четвертого шахматиста D с одним из шахматистов А, В или С сразу же появится шахматист, имеющий 1 очко. Действительно, пусть, например, шахматист D померился силами с шахматистом А и проиграл ему. Тогда, согласно принятому правилу, шахматист В, выигравший у шахматиста А, получает 1 очко. Если же шахматист D выиграет у шахматиста А, то тогда уже он получит 1 очко за победу шахматиста А над шахматистом С.
Таким образом, Григорову удалось победить в одной или в двух встречах.
Предположим, что Григоров победил лишь в одной встрече (две проиграл). Если бы проигравший ему соперник выиграл всего лишь одну встречу, то чемпионом турнира также был бы и Маричев. Поэтому проигравший Григорову соперник (Антонюк или Даринцев) в двух своих остальных встречах должен оказаться победителем, за что Григорову должно быть засчитано 2 очка.
Предположим сначала, что Григоров победил Даринцева, который, в свою очередь победил Антонюка и Маричева. Если бы при этом Антонюк выиграл у Маричева, то он с 2 очками также как и Григоров был бы чемпионом турнира, а если бы ему проиграл, то с 2 очками был бы чемпионом турнира Маричев.
Значит, если Григоров победил лишь в одной встрече, то это могла быть его встреча с Антонюком. Поскольку при этом он Даринцеву проиграл, то количества начисленных игрокам очков определялись бы результатом встречи Даринцев—Маричев. В таком случае победа Даринцева над Маричевым принесла бы ему в итоге 2 очка (напомним, столько же, сколько и чемпиону Григорову). Если бы Даринцев проиграл Маричеву, то в этом случае Маричев набрал бы 2 очка.
Следовательно, предположение о победе Григорова лишь в одной встрече ошибочно: Григоров победил и Антонюка, и Даринцева. Поэтому Маричев, победивший Григорова, набрал не менее двух очков. Поскольку Григоров — единственный чемпион, то набрал он не менее трех очков. Изобразим на рис. 3 уже известные результаты встреч.
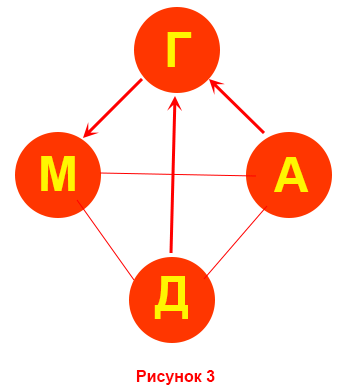
Так как у Григорова в итоге оказалось не менее трех очков, то один из побежденных им соперников (Антонюк и Даринцев) выиграл 2 раза, а второй — не менее одного раза.
Даринцев дважды выиграть не мог, поскольку в этом случае он набрал бы 2 очка (столько же, сколько и Маричев), а у Антонюка было бы лишь 1 очко и поэтому именно он занял бы последнее место в турнире.
Следовательно, Антонюк победил Даринцева и Маричева, а Даринцев - победителя Григорова - Маричева.
Окончательный итог турнира приведен на рис. 4.
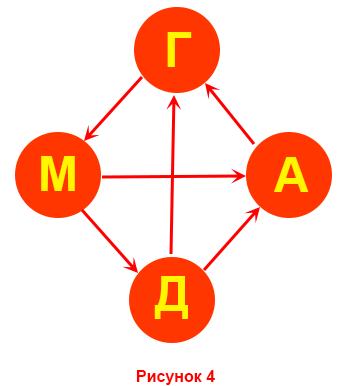
Итак, Григоров в турнире набрал 3 очка, Антонюк и Маричев по 2 и Даринцев — 1.















