Определить вершины квадрата с помощью циркуля

Решение. Пусть а — известная сторона квадрата. Поместив ножку циркуля в некоторую точку О, проведём радиусом а дугу, на которой, выбрав произвольную точку А, отложим АВ = ВС = CD

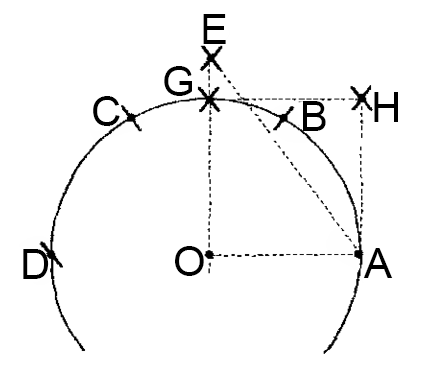
Точки А, В, С и D являются вершинами правильного шестиугольника, вписанного в окружность радиуса а. Расстояние между точками А и С равно а√3 — стороне вписанного в указанную окружность равностороннего треугольника. Из точек А и D опишем дуги радиусом АС и отметим их точку пересечения — Е.

Так как АЕ² = ОЕ² + OA², то ОЕ = √3а² - а² =а√2. Значит, если из точек А и D описать дуги радиусом ОЕ, то они пересекутся на дуге ABCD в точке G — вершине квадрата, вписанного в окружность радиуса а.

Определить местоположение четвертой вершины Н искомого квадрата теперь уже легко: достаточно из точек А и G провести дуги радиуса а и найти их пересечение — точку Н.