Что такое тела Архимеда?
Телами Архимеда называют полуправильные выпуклые многогранники.
Что значит полуправильные?
Полуправильные многогранники в отличие от правильных (платоновых тел) состоят из двух и более типов граней - правильных многоугольников, примыкающих к одной вершине. У правильных многогранников к каждой вершине примывает только один тип правильных многоугольников.
Кроме того, у архимедовых тел для любой пары вершин существует симметрия многогранника (то есть движение, переводящее многогранник в себя), переводящая одну вершину в другую.
А что значит выпуклый многогранник и чем от отличается от невыпуклого?
Выпуклый многогранник лежит с одной стороны от плоскости любой из своих граней. Если соединить любые две точки, принадлежащие выпуклому многограннику, то полученный отрезок будет полностью принадлежать этому многограннику.
Вот примеры невыпуклых многогранников:
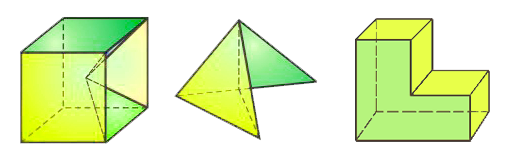
Невыпуклые многогранники
Итак, архимедовы тела - это выпуклые полуправильные многогранники. Тел Архимеда всего тринадцать.
| Архимедово тело | Как выглядит (полупрозрачный). Кликните для вращения |
Грани | Количество вершин | Количество рёбер | В каждой вершине сходятся | |
|---|---|---|---|---|---|---|
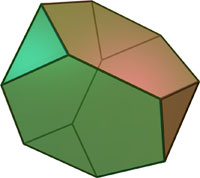
| 1 | Усечённый тетраэдр |
4 треугольника, 4 шестиугольника |
12 | 18 | 3, 6, 6 | |
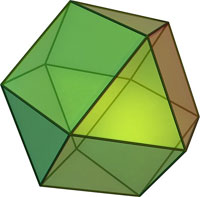
| 2 | Кубооктаэдр |
8 треугольников, 6 квадратов |
12 | 24 | 3, 4, 3, 4 | |
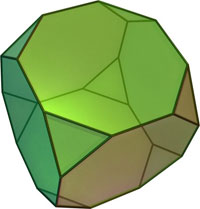
| 3 | Усечённый куб |
8 треугольников, 6 восьмиугольников |
24 | 38 | 3, 8, 8 | |
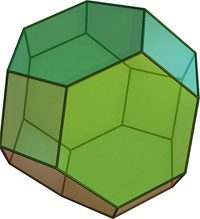
| 4 | Усечённый октаэдр |
6 квадратов, 8 шестиугольников |
24 | 36 | 4, 6, 6 | |
| 5 | Ромбокубооктаэдр |
8 треугольников 18 квадратов ( 6 — в кубическом положении, 12 — в ромбическом) |
24 | 48 | 3, 4, 4, 4 | |
| 6 | Усечённый кубооктаэдр |
12 квадратов, 8 шестигольников, 6 восьмиугольников |
48 | 72 | 4, 6, 8 | |
| 7 | Плосконосый куб |
32 треугольника, 6 квадратов |
24 | 60 | 3, 3, 3, 3, 4 | |
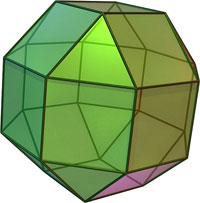
| 8 | Икосододекаэдр |
20 треугольников, 12 пятиугольников |
30 | 60 | 3, 5, 3, 5 | |
| 9 | Усечённый додекаэдр |
20 треугольников, 12 десятиугольников |
60 | 90 | 3, 10, 10 | |
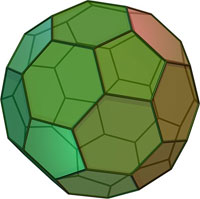
| 10 | Усечённый икосаэдр |
 |
12 пятиугольников, 20 шестиугольников |
60 | 90 | 5, 6, 6 |
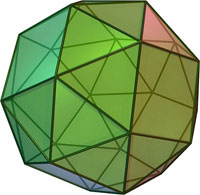
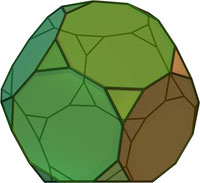
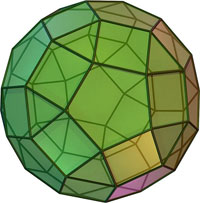
| 11 | Ромбоикосододекаэдр |
20 треугольников, 30 квадратов, 12 пятиугольников |
60 | 120 | 3, 4, 5, 4 | |
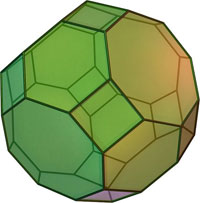
| 12 | Ромбоусечённый икосододекаэдр |
30 квадратов, 20 шестиугольников, 12 десятиугольников |
120 | 180 | 4, 6, 10 | |
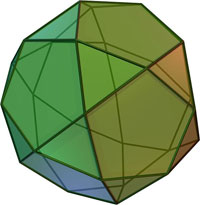
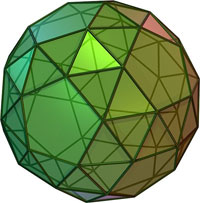
| 13 | Плосконосый додекаэдр |
80 треугольников, 12 пятиугольников |
60 | 150 | 3, 3, 3, 3, 5 |