Открытие Ф. Крика

Хорошо помню тот день, когда мы накануне нового, 1961 года собрались на очередной семинар нашего отдела. Незадолго до этого руководитель семинара Виктор Юлианович Гаврилов предложил больше не реферировать статьи о генетическом коде. Причина была все та же: проблема запутана, путей экспериментальной проверки не находится. Перед началом семинара, когда в последних рядах шла ожесточенная борьба претендентов на «спальные» места, Володя Пермогоров вдруг вялым голосом сказал, что вчера узнал от приятеля, будто биохимик Пауль Доти прислал письмо, в котором сообщил, что Крик раскрыл природу кода. Но больше он ничего сказать не смог.

А через несколько дней Гаврилов собрал внеочередной семинар, чтобы сделать важное сообщение.

Обычно весьма невозмутимый Виктор Юлианович на этот раз был натянут как струна. Вез каких-либо предисловий он начертил на доске линеечки, а как только над ними появились три значка — r-II, А и В,— все поняли, что речь пойдет об r-II-мутантах. Тут-то мы и услышали о работе Крика. Вернее, Крика, Барнета, Бреннера и Ватс-Тобина, потому что, как рассказывают злые языки, Крик, оправдывая профессию теоретика, обычно сидит в своей комнате в полнейшем уединении и, поигрывая карандашиком, рисует схемы опытов, а первоклассные экспериментаторы претворяют в жизнь теоретические упражнения своего теоретического бога. «Бригада Крика» и он сам оказались на высоте и на этот раз. Идея была предельно проста, ее обоснование предельно лаконично.

Замысел работы возник у ученого давно. В нескольких его статьях есть прямые намеки на смысл будущей работы. Но воплотить эту мысль — немного позже вы познакомитесь с ней — мешало одно обстоятельство.. Крику нужно было ухитриться по своему желанию вставлять в ДНК одно лишнее основание, а затем с такой же легкостью вынимать одно основание. Совсем недавно мы вспоминали длину нуклеотида (основание + сахар + фосфат) и говорили, что она равна 3,4 А. Это, конечно, ускользающе мало для того, чтобы легко манипулировать с основаниями. Возможно, что идея Крика так и осталась бы пылиться в архивах, но ему (и всей науке) повезло. Был найден мутаген — его именовали профлавином,— который делал именно то, что нужно было Крику. Он либо вышибал одно (или два) основания из ДНК, либо вставлял одно (или два) основания в ДНК. Его вкусы — и это самое главное — были всегда постоянными. Профлавин всегда вставлял или вышибал одно и то же число нуклеотидов (ученым было трудно определить, с одним или с парой оснований манипулирует профлавин, но это не имело значения).

Теперь Крик держал в руках все ключи к проверке гипотезы: изучение г-II-мутаций фага Т4 было закончено, профлавин мог легко вставить и вынуть из ДНК этого фага основание в участке г-II. Метод тонкого генетического анализа Бензера позволял точно определить место нарушения (вставки или выпадения основания).

Ученые приступили к опытам. Они взяли нормальный фаг Т4. Обработали его профлавином и получили точечную мутацию в гене г-II В — фаг перестал расти на культуре кишечной палочки линии К. Мутация (ее обозначили значком FCO — по первым буквам имени Крика—Francis Crick; «О» означает нулевую мутацию) могла быть следствием либо выпадения, либо вставки основания. Но решить, какая из альтернатив верна, ученые не могли и обозначили ее знаком «+», то есть вставление. Как вы увидите дальше, результат нисколько не изменится, если эта мутация на самом деле не «+», а «—».

Итак, первая мутация FCO была получена, и ее назвали «+». С помощью метода генетического картирования определили точное место FCO на карте цистрона В области г-II.
После этого обработали профлавином не дикий штамм вируса, а этот мутант FCO, и... фаг начал расти на культуре К. Он снова стал диким. Что это значит? Мутантный фаг мог стать диким после того, как первоначальное изменение (неважно, вставка или выпадение) было исправлено. Если придерживаться обозначений Крика, то плюс сменился минусом, другими словами — лишнее вставленное основание профлавин вышиб. Проверить с помощью метода Бензера, восстановлен ли первоначальный порядок оснований в месте, где раньше была мутация FCO, теперь было проще простого.

Но проверка показала, что старая мутация FCO осталась на месте, а рядом с ней возникла новая мутация. Следовательно, вторая подавила действие первой, стала, как говорят генетики, супрессором первой мутации. Крик предлагает весьма остроумную гипотезу молекулярной природы супрессора. Представим себе непрерывную запись какой-то генетической фразы. Учитывая, что каждое слово в книге наследственности состоит из трех букв, а Крик оставался верен своему сплошному коду, фразу можно написать так:

ABC ABC ABC ABC ABC ABC ABC ABC ABC

Неважно, что в этой фразе все слова одинаковы — ABC, это поможет быстрее разобраться в задаче. Итак, есть фраза. Вставим в нее в любом произвольно выбранном месте какую-то букву (например В), но читать по-прежнему будем одну тройку букв за другой. Тогда все слова после вставленной буквы потеряют смысл:

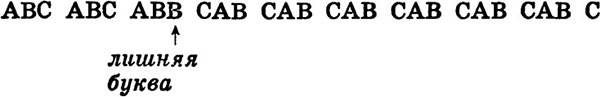
Можно ли исправить большую часть фразы, не вынимая именно эту лишнюю букву В? Можно, если сделать противоположную операцию — по-соседству с В вынуть любую другую букву. Получим:

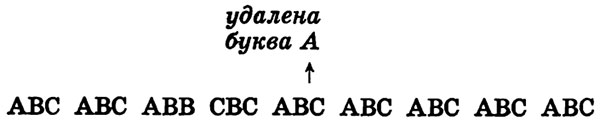
Как видите, все в порядке. Почти на всем протяжении (за исключением участка от вставленной буквы В до вынутой буквы А — ВВСВС) фраза восстановила свой первоначальный смысл.

Если теперь припомнить, что нередко даже половина белка может быть отброшена, а активность его сохранится (только не был бы поврежден активный центр фермента), то станет ясно: вероятность полного восстановления смысла при таком повреждении достаточно велика.

Значит, если согласиться с двумя предположениями Крика: код трехбуквенный, слова читаются от какой-то начальной точки без перерыва, то причина возникновения супрессора станет понятной.

Но Крика не удовлетворяют всякие там «допустим», «если согласиться». Ставится еще несколько опытов, чтобы доказать верность гипотезы, и тогда хочешь не хочешь — с ней придется согласиться всем. Прежде всего проверяется верность предложенного механизма работы супрессоров. Дважды мутировавший фаг (мутация FCO и ее супрессор) снова обрабатывают профлавином и опять получают фаги, не растущие на К. Генетическое картирование дает такой ответ: рядом с двумя мутациями «+» и «—» возникла третья.

Что же, снова «+»? Супрессор первого супрессора?

И вот в пробирках исследователей накапливаются новые супрессоры супрессоров, к ним получают еще супрессоры и т. д. Пока все обнаруженные факты можно просто объяснить с позиций предложенного механизма супрессии. Как только накопилось много разных плюсов и минусов, стало возможным проверить их свойства простым способом. Если плюсы действительно плюсы, а минусы действительно минусы, то, скрестив любой плюс с любым минусом, получишь восстановление нормального чтения.
Ученые проводят одно скрещивание за другим и ни в одном случае не получают противоречия с гипотезой. Гипотеза доказана!

Крик предлагает схему предельно простого опыта, который даст ответ на вопрос, сколько же букв входит в кодовые слова природы (кодоны): три, как предположил Гамов, или больше? Если кодон состоит из трех букв, то тогда, вынув сразу три буквы или вставив три буквы одновременно, получим почти неизменную фразу. Если же код не трехбуквенный, а какой-то иной, тогда другое число вставлений и выпадений приведет к сохранению чтения.

Наступает решающая часть опыта. Скрещиваются два фага, несущие две «+» мутации. Что, если код все-таки двухбуквенный? Но ничего подобного: совмещение двух близко лежащих плюсов не восстанавливает правильность чтения. Фаги, несущие два плюса, не размножаются на культуре кишечной палочки К. Теперь к двум плюсам добавляют еще одну «+» мутацию: сейчас в ДНК фага рядом сидят три плюса. Нарисуем снова фразы и изобразим последовательное введение трех плюсов в ДНК фага.

Исходная фраза: ABC ABC ABC ABC ABC ABC ABC ABC ABC
Первая
вставленная буква: ABC ABC AAB CAB CABC CAB CAB САВ CAB
Вторая
вставленная буква: ABC ABC AAB CAA BCA BCA BCA BCA BCA
Третья
вставленная буква: ABC ABA CAA BCA ABC ABC ABCAABC ABC

Чтение, нарушенное первым и вторым вставлением, должно восстановиться после третьей добавки. Конечно, если только три испорченных слова ABA CAA BCA не окажутся роковыми для клетки. Но вряд ли это может случиться. Понимаем же мы речь картавого человека!

Все сомнения рассеиваются после первого же опыта. Ученые высевают такой трижды плюсовой фаг на чашки Петри. Через несколько часов на бактериальных газонах явственно проступают контуры бляшек. Проходит положенное время, и все сомнения отпадают — видны четкие бляшки дикого типа. Удача! Код трехбуквенный!