Как был построен самый многоугольный многоугольник?
Для современного школьника не составляет труда построить правильный многоугольник. Каждый может начертить треугольник, квадрат, пятиугольник... Даже если число сторон возрастет до нескольких десятков, решение задачи потребует лишь чуть больше терпения и усидчивости. Но что делать, если речь зайдет о тысячах и десятках тысяч сторон?
В университете немецкого города Геттингена произошел случай из разряда курьёзных. О нём рассказал известный английский математик Д. Литтлвуд. Один не в меру навязчивый аспирант вывел своего руководителя из терпения. Желая хоть немного отдохнуть от дотошного ученика, профессор сказал ему: «Идите и разработайте построение правильного многоугольника с 65 357 сторонами».
Профессор надолго избавился от ученика, ведь старательный немец принял задание руководителя всерьез. Он вернулся только через 20 лет с соответствующим построением. И сейчас это чудо усидчивости хранится в архивах Геттингенского университета.
Другие источники говорят, что эта история - всего лишь шутка, придуманная Литтлвудом на основе реального события: построение действительно существует и его оригинал на самом деле хранится в библиотеке Геттингенского университета. Это построение произвел математик Иоганн Густав Гермес в 1894 году, потратив на это более 10 лет. Рукопись занимает более 200 страниц, содержится в огромном чемодане и по причине своих необъятных размеров никогда не была опубликована.
Кстати...
Почему именно 65 537 сторон? Разумеется, профессор взял это число не с потолка. Дело в том, что еще в 1836 году выдающийся немецкий математик Карл Фридрих Гаусс доказал, что правильный многоугольник можно построить, пользуясь лишь циркулем и линейкой, если число его вершин равно простому числу Ферма, т. е. числу вида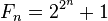 
где n — неотрицательное целое число.
А 65 537 - это самое большое из известных чисел Ферма:
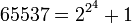
Как же выглядит это чудо человеческой мысли - шестидесятипятитысячпятисоттридцатисемиугольник? Внешне он практически неотличим от окружности! Ведь его центральный угол, то есть угол с вершиной в центре окружности, ничтожно мал - 0°0'19"77508888. Если нарисовать 65537-угольник с длиной одной стороны 1 см, то его диаметр будет больше 200 м.
