ВВоткнутые линии и другие обманы зрения

Начерченная на рис. 1 группа булавок не представляет на первый взгляд ничего особенного. Но поднимите книгу на уровень глаз и, закрыв один глаз, смотрите на эти линии так, чтобы луч зрения скользил вдоль них. (Глаз нужно поместить в той точке, где пересекаются продолжения этих прямых.) При таком рассматривании вам покажется, что булавки не начерчены на бумаге, а воткнуты в нее стоймя. Отводя голову немного в сторону, вы увидите, что булавки словно наклоняются в ту же самую сторону.

Рис. 1.
Поместите один глаз (закрыв другой) приблизительно в той точке, где пересекаются продолжения этих линий.
Вы увидите ряд булавок, словно воткнутых в бумагу.
При легком перемещении рисунка из стороны в сторону булавки кажутся качающимися.

Эта иллюзия объясняется законами перспективы: линии начерчены так, как должны были бы проектироваться на бумагу отвесно торчащие воткнутые булавки, когда на них смотрят описанным выше образом.

Способность нашу поддаваться зрительным обманам вовсе не следует рассматривать только как недостаток зрения. Она имеет и свою весьма выгодную сторону, о которой часто забывают. Дело в том, что, если бы глаз наш неспособен был поддаваться никаким обманам, не существовало бы живописи и мы лишены были бы всех наслаждений изобразительных искусств. Художники широко пользуются этими недостатками зрения. "На сей обманчивости все живописное художество основано, — писал гениальный ученый XVIII века Эйлер в своих знаменитых "Письмах о разных физических материях". — Ежели бы мы привыкли судить о вещах по самой истине, то бы сие искусство (т. е. художество) не могло иметь места, равно как когда бы мы были слепы. Всуе художник истощил бы все свое искусство на смешение цветов; мы бы сказали: вот на сей доске красное пятно; вот голубое, здесь черное и там несколько беловатых линий; все находится на одной поверхности, не видно на ней никакого в расстоянии различия и не можно бы было изобразить ни единого предмета. Что бы на картине ни написано было, так бы нам казалось, как письмо на бумаге... При сем совершенстве не были ли бы мы сожаления достойны, лишены будучи удовольствия, которое приносит нам ежедневно столь приятное и полезное художество?"

Оптических обманов очень много, можно наполнить целый альбом различными примерами таких иллюзий. Многие из них общеизвестны, другие менее знакомы. Привожу здесь еще несколько любопытных примеров оптических обманов из числа менее известных. Особенно эффектны иллюзии рис. 2 и 3 с линиями на сетчатом фоне: глаз положительно отказывается верить, что буквы на рис. 2 поставлены прямо. Еще труднее поверить тому, что на рис. 43 перед нами не спираль. Приходится убеждать себя в этом непосредственным испытанием: поставив острие карандаша на одну из ветвей мнимой спирали, кружить по дугам, не приближаясь и не удаляясь от центра.

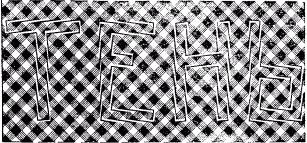
Рис. 2. Буквы поставлены прямо.


Рис. 3. Кривые линии этой фигуры кажутся спиралью; между тем это окружности, в чем легка убедиться, водя по ним заостренной спичкой.

Точно так же, только с помощью циркуля, можем мы убедиться, что на рис. 4 прямая AC не короче АВ.

Рис. 4. Расстояния AB и AC равны, хотя первое кажется больше.

Сущность остальных иллюзий, порождаемых рисунками 5, 6, 7, 8, объяснена в подписях под ними. До какой степени сильна иллюзия рис. 7, показывает следующий курьезный случай: издатель одного из предыдущих изданий моей книги, получив от цинкографии оттиск этого клише, счел клише недоделанным и готовился было уже возвратить его в мастерскую, чтобы счистить серые пятна на пересечении белых полос, когда я, случайно войдя в комнату, объяснил ему, в чем дело.

Рис. 5. Косая линия, пересекающая полоски, кажется изломанной.


Рис. 6. Белые и черные квадраты равны, так же как и круги.


Рис. 7. На пересечении белых полос этой фигуры появляются и исчезают, словно вспыхивая, сероватые квадратные пятнышки. В действительности же полоски совершенно белы по всей длине, в чем легко убедиться, закрыв бумагой прилегающие ряды черных квадратов. Это - следствие контрастов.


Рис. 8. На пересечении черных полос появляются сероватые пятна.