а) Цепочка с незамкнутыми концами состоит из 13 звеньев. Каждое звено имеет массу 1 грамм и может быть разомкнуто.
Какое минимальное количество звеньев цепочки нужно разомкнуть, чтобы, пользуясь образовавшимися частями цепочки как разновесами, можно было бы на чашечных весах уравновесить груз, масса которого в граммах выражается любым целым числом от 1 до 13 ?
б) Если цепочка с незамкнутыми концами состоит из N однограммовых звеньев, то какое их минимальное количество достаточно разомкнуть, чтобы, используя полученные части цепочки как разновесы, можно было бы на чашечных весах уравновесить груз, масса которого в граммах выражается любым целым числом от 1 до N?
а) 1 звено. Следует разомкнуть четвертое звено цепочки. Образуются разновесы в 1, 3 и 9 граммов.
Действительно, любое целое число отрезка [1,13] можно представить в виде алгебраической суммы чисел 1, 3 и 9 (знак минус означает, что соответствующий разновес помещается на ту же чашку весов, что и взвешиваемый груз).
1 = 1, 2 = 3 - 1; 3 = 3; 4 = 3 + 1, 5 = 9 - 3 - 1, 6 = 9 - 3, 7 = 9 -3 + 1, 8 = 9 - 1, 9 = 9, 10 = 9 + 1; 11 = 9 + 3 + 1, 12 = 9 + 3, 13 = 9 + 3 + 1.
б) Наименьшее количество звеньев цепочки длины N, размыкания которых достаточно для выполнения требования задачи, равно наименьшему натуральному числу, при котором выполняется неравенство
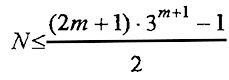 (1)
Доказательство
(1)
Доказательство. После размыкания цепочки в m местах, дополнительно к m раскрытым звеньям будут получены еще m + 1 куска этой цепочки, состоящие из n
1, n
2, ..., n
m, n
m + 1 звеньев. Очевидно, если цепочка состояла из N звеньев, то
m + n
1 + n
2 + ... + n
m + 1 = N, (2)
а порядковый номер t
i ее i-го размыкаемого звена можно вычислить по формуле
t
i = t
i-1 + n
i + 1 для любого i = 2, 3, ...,m, (3)
а t
1 = n
1 + 1. Поэтому, приняв во внимание равенство (2),
t
m + n
m+1 = N (4)
Не ограничивая общности, можно считать, что
n
1 ≤ n
2 ≤...≤ n
m
(длину (массу) n
m + 1 последнего куска N-звенной цепочки можно определить из равенства (2) или (4)).
Используя m разомкнутых звеньев цепочки на чашечных весах, можно уравновесить груз, выраженный в граммах любым целым числом от 1 до m.
Если же использовать m разомкнутых звеньев цепочки и ее n
1 -звенный кусок, то можно уравновесить груз, выраженный в граммах любым целым числом из интервала и [1,m] и [n
1 - m, n
1 + m] (здесь предполагается, что n
1 > m). Если при этом n
1 = 2m + 1, то, используя лишь указанные части цепочки, можно уравновесить груз, масса которого в граммах выражается любым целым числом из интервала [1, Зm+1]. Этот интервал представляет собой объединение непересекающихся интервалов [1,m] и [n
1 - m, n
1 + m] и имеет длину m + n
1
= 3m + 1.
Руководствуясь аналогичным правилом, можно подобрать длину n
2 второго куска цепочки: значение n
2 должно быть таким, чтобы, во-первых, используя лишь m разомкнутых звеньев цепочки и ее n
1- и n
2-звенные куски, можно было бы уравновесить груз, масса которого в граммах выражается любым целым числом из интервала [1, n
2 + n
1 + m] и, во-вторых, чтобы интервал [n
2 - n
1 - m, n
2 + n
1 + m] не имел общих точек с непересекающимися интервалами [1,m] и [n
1 - m, n
1 + m]. Эти условия, очевидно, выполняются в том и только в том случае, когда n
2 - n
1 - m = n
1 + m + 1, то есть, если n
2 = 2n
1 + 2m + 1 = 3n.
В общем случае длина n
i+1 (i+1)-го куска цепочки должна быть такой, чтобы, используя лишь m ее разомкнутых звеньев и куски длины {n
j}, j = 1, ..., i, можно было бы уравновесить груз, выраженный в граммах
любым целым числом из интервала
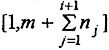
, и чтобы интервал
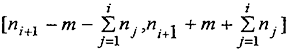
не имел общих точек с интервалом
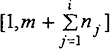
. Отсюда следует, что
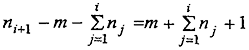
, и поэтому
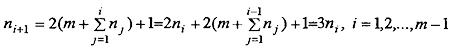
(6)
Итак, используя m разомкнутых звеньев заданной цепочки и ее куски длиной n
1, n
2 ..., n
m, на чашечных весах можно уравновесить груз, величина которого в граммах принимает любое целочисленное значение из интервала
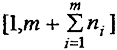
. Учитывая соотношения (6) и то, что n
1 = 2m + 1, максимальная масса P
m такого груза равна
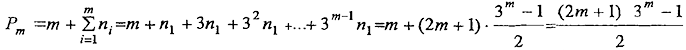
(7)
Пусть P — масса в граммах уравновешиваемого груза, выражаемая любым целым числом из интервала [1, N]. Достаточно рассмотреть лишь случай, когда P > P
m, т. е. Р = P
m + p, где p — произвольное целое число отрезка [1, n
m+1].
Предположим для определенности, что на левую чашку весов поместили указанный груз P, а на правую, чтобы этот груз уравновесить, (m+1)-й кусок цепочки и некоторое сочетание разновесов общей массой, составленной из имеющихся разомкнутых звеньев и кусков цепочки. Чашки весов находятся в равновесии тогда и только тогда, когда выполняется равенство Р = n
m+1 + x, т. е., если
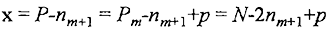
(8)
Отсюда, так как 1 ≤ p ≤ n
m+1, имеем
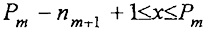
(9)
Условие, выражающее возможность составить из имеющихся разновесов (без последнего (m + 1)-го куска цепочки) массу х, состоит в выполнении неравенства
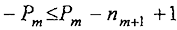
(10)
(отрицательное значение х означает, что система разновесов размещается вместе с грузом P на левой чашке весов). Из этого неравенства следует требование n
m+1 ≤ 2P
m + 1, которое, учитывая равенства P
m + n
m+1 = N и (7), эквивалентно неравенству (1)
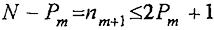
и, значит,
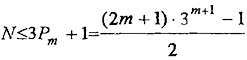
(11)
Таким образом, для заданного N можно вычислить минимальное значение m, для которого выполняется неравенство (11), и затем уже по формуле (6) вычислить «длины» кусков {n
i} требуемых разновесов, а по формуле (3) — порядковые номера размыкаемых звеньев цепочки.
Заметим, правая часть N
max неравенства (11) есть точная верхняя оценка максимального числа N звеньев у цепочки, размыкание m звеньев которой позволит выполнить требование задачи. Приведем значения N
max для нескольких значении m.
| m |
1 |
2 |
3 |
4 |
5 |
| Nmax |
13 |
67 |
283 |
1093 |
4009 |
Из этой таблички следует, что для изготовления указанных в задаче разновесов из цепочек, состоящих, например, из 60 и 150 звеньев, достаточно разомкнуть не более двух и трех звеньев соответственно. Соотношения (3) и (6) позволяют определить номера этих звеньев: в 60-звенной цепочке необходимо разомкнуть 6-е и 22-е звенья, а в 150-звенной - 8-е, 30-е и 94-е. При этом из 60-звенной цепочки будут получены 5 разновесов, состоящих из 1, 1, 5, 15 и 38 звеньев, а из 150-звенной цепочки - 7 разновесов, в которых соответственно 1, 1, 1, 7, 21, 63 и 56 звена.
Покажем, как при помощи разновесов, изготовленных из 60-звенной цепочки, на чашечных весах можно уравновесить груз, масса которого в граммах может принимать любое целочисленное значение между 22 и 38 (уравновешивание груза другой массы, допустимой в задаче, сложности не вызывает).
23 = 38 - 15
24 = 38 - 15 + 1
25 = 38 - 15 + 1 + 1
26 = 38 - 15 + 5 - 1 - 1
27 = 38 - 15 + 5 - 1
28 = 38 - 15 + 5
29 = 38 - 15 + 5 + 1
30 = 38 - 15 + 5 + 1 + 1
31 = 38 - 5 - 1 -1
32 = 38 - 5 - 1
33 = 38 - 5
34 = 38 - 5 + 1
35 = 38 - 5 + 1 + 1
36 = 38 - 1 - 1
37 = 38 - 1


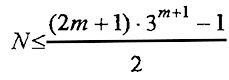 (1)
(1)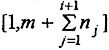 , и чтобы интервал
, и чтобы интервал 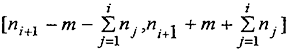 не имел общих точек с интервалом
не имел общих точек с интервалом 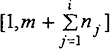 . Отсюда следует, что
. Отсюда следует, что 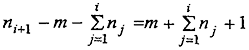 , и поэтому
, и поэтому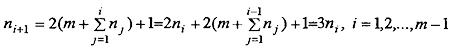 (6)
(6)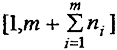 . Учитывая соотношения (6) и то, что n1 = 2m + 1, максимальная масса Pm такого груза равна
. Учитывая соотношения (6) и то, что n1 = 2m + 1, максимальная масса Pm такого груза равна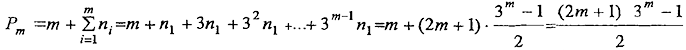 (7)
(7)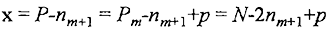 (8)
(8)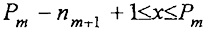 (9)
(9)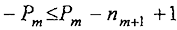 (10)
(10)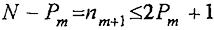
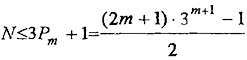 (11)
(11)








